安志萍：主成分分析法（PCA）在高维医疗数据降维中的应用研究

一 研究背景

　　在医疗健康领域，高维医疗数据的涌现及其在诊断与预测中的作用愈发关键。这些数据涵盖了影像、基因、生理参数等多源信息，极大地拓展了医疗数据的维度，为疾病预防、诊断和治疗带来新机遇。它们能助力医生从海量数据中精准提取有价值信息，提升诊断准确性和效率；通过挖掘分析，还能发现疾病新机制，推动医疗科技进步，实现医疗服务个性化与精准化，提高质量和患者满意度。然而，高维数据处理分析面临诸多挑战，如存储空间需求大、计算复杂度高、维度灾难，以及数据可解释性与可视化等难题，此外如何确保数据解读一致性和准确性也至关重要。

　　有效处理分析高维数据、提取出有价值信息，是当前医疗领域亟待解决的关键问题。这不仅需要运用高级数据处理分析技术，揭示数据内在规律和关系，为医疗决策提供科学依据，还需深入理解高维数据的特点与挑战，从而优化算法、提升数据的利用效率。这是一项多学科交叉合作的挑战，也是大数据时代医疗领域的重要机遇。

　　在此背景下，主成分分析（PCA，Principal Component Analysis）作为一种常用的降维工具，其优势愈发凸显。PCA是基于多元线性代数和正交变换，旨在从众多变量中寻找出能最大化解释数据方差的主要主成分。这些主成分是原始数据在高维空间的投影，可以保留主要信息，去除噪声和冗余。PCA在数据挖掘、图像处理、生物信息学等领域应用已较为广泛。

　　本研究以口腔癌数据集为研究对象，旨在深入探究主成分分析（PCA）在高维医疗数据降维中的基本原理与计算过程，并分析其对模型运行效率和精度的影响，为高维医疗数据的降维及诊断精度的提升提供理论支持和实践指导。

二 PCA的基本原理与算法

　　1.基本原理

　　主成分分析（PCA）的基本数学原理主要围绕协方差矩阵、特征值和特征向量展开，这些概念是其实施的核心。简单来说，原始数据矩阵中的每个变量是一个独立的列向量，协方差矩阵则刻画了这些变量之间的相关性。PCA通过正交变换，将原始数据矩阵转换为新的矩阵，其中每一列（即每个主成分）是原始列向量的线性组合，且各主成分相互正交，不存在线性相关性，从而最大化地保留了原始数据的信息。

　　2.计算过程

　　首先，标准化数据。对数据进行标准化，以消除不同特征量纲对总体方差的影响。

　　其次，计算协方差矩阵。该矩阵反映了变量之间的相关性。

　　第三，特征分解。将协方差矩阵分解为特征值和特征向量。特征值和特征向量是PCA的核心，特征值表示每个主成分所能解释的方差大小，而特征向量则确定了主成分的方向。

　　第四，选择主成分。选择方差累计贡献率最高的特征向量作为主成分，这些主成分能够最大化地保留数据信息。

　　通过以上计算步骤，可将原始数据投影到这些特征向量上，即实现降维，从而得到一组新的、相互独立的特征变量，这些变量能够高效地保留原始数据的变异性，同时显著降低数据维度。

三 PCA在医疗诊断中示例应用

　　本研究首先利用随机森林分类算法构建口腔癌预测模型，并采用PCA对高维数据集进行降维处理，设定保留95%的方差。通过对比降维前后模型的预测精准度、训练效率以及内存资源消耗等，深入探究PCA降维技术在高维数据中的应用效果。技术工具采用：Python 3.7 + PyCharm 2022.2（Community Edition）。

　　1.数据集介绍

　　本研究采用的口腔癌数据集来自Kaggle，提供了全球口腔癌病例的详细结构化概述。数据集基于真实世界口腔癌统计数据，与全球健康研究报告保持一致。

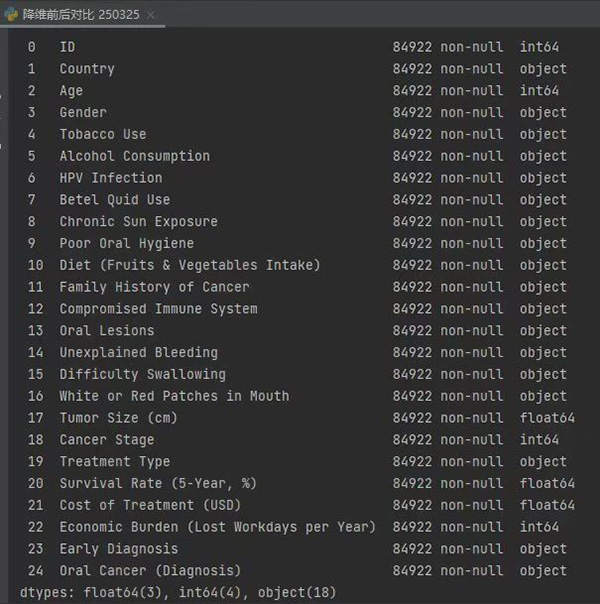
　　该数据集共有25个特征变量，说明如下：（1）ID 唯一标识符、（2）Country患者国籍、（3）Age患者年龄、（4）Gender性别、（5）Tobacco Use烟草使用、（6）Alcohol Consumption酒精摄入、（7）HPV Infection  HPV感染、（8）Betel Quid Use槟榔使用、（9）Chronic Sun Exposure长期日光暴露、（10）Poor Oral Hygiene口腔卫生不良、（11）Diet (Fruits & Vegetables Intake) 饮食（果蔬摄入量）、（12）Family History of Cancer癌症家族史、（13）Compromised Immune System免疫功能缺陷、（14）Oral Lesions口腔病变、（15）Unexplained Bleeding不明原因出血、（16）Difficulty Swallowing吞咽困难、（17）White or Red Patches in Mouth口腔白/红斑块、（18）Tumor Size (cm) 肿瘤尺寸、（19）Cancer Stage癌症分期、（20）Treatment Type治疗方式、（21）Survival Rate (5-Year, %)五年生存率、（22）Cost of Treatment (USD) 治疗成本（美元）、（23）Economic Burden (Lost Workdays per Year) 经济负担（年误工天数）、（24）Early Diagnosis 早期诊断，和1个目标变量Oral Cancer (Diagnosis) 口腔癌诊断。

　　2.数据描述性分析

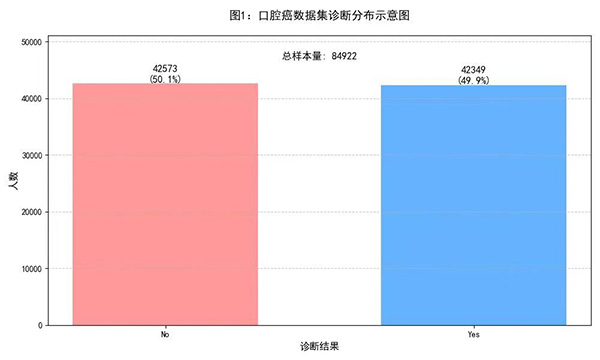
　　数据集包含84922个样本，其中口腔癌患者42349例，占比49.9%，非口腔癌患者42573例，占比50.1%。数据分布较为平衡，有助于避免因数据不平衡而导致的模型偏差。该数据集无空值记录，也无重复记录，这表明数据质量较高，确保了数据的完整性和一致性，能够有效支持后续的分析和建模工作。

3.数据预处理

首先，对数据集中的分类变量进行标签编码（Label Encoding）。例如，将“Tobacco Use”和“Alcohol Consumption”等以“Yes/No”表示的变量，以及“Gender”以“Male/Female”表示的变量，均转换为“0/1”数值形式。

其次，采用目标编码器（TargetEncoder）对数据集中的多分类无序变量进行编码。例如，将“Country”以国家名称表示的变量、“Diet (Fruits & Vegetables Intake)”以“Low/Moderate/High”表示的变量，以及“Treatment Type”以“Surgery/Radiation/Chemotherapy/Targeted Therapy/No Treatment”等表示的变量，均转换为数字形式。

最后，利用数据标准化工具StandardScaler对数据集中的数值型特征进行标准化处理。这些特征包括“Tumor Size (cm)”、“Cost of Treatment (USD)”和“Economic Burden (Lost Workdays per Year)”等。

4.PCA降维前后医疗诊断模型的构建与对比

本研究采用随机森林分类算法构建口腔癌预测诊断模型，并将数据集按30%的比例划分为训练集和测试集。随后，引入主成分分析（PCA）进行降维处理，设定特征向量的选择标准为方差累计贡献率超过95%，以确保数据的主要信息得以保留。

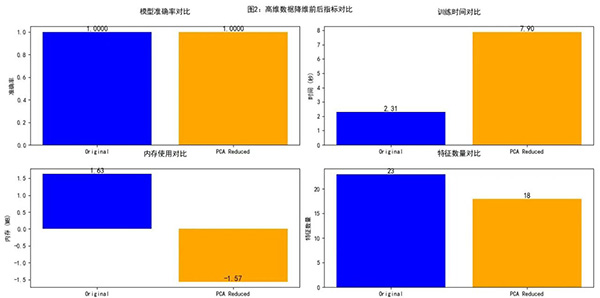
部分指标对比结果如图2所示。从图中可知，降维前后模型的准确率均为1，表明PCA降维并未对模型的预测精度产生负面影响，模型仍保持了较高的诊断准确性。然而，训练时间从2.31秒增加至7.90秒，这主要是由于PCA降维过程本身需要额外的计算资源，导致整体训练时间有所延长。内存使用量从1.63MB降至-1.57MB，这一变化反映了降维后特征数量的减少，使得模型在训练和预测过程中占用的内存资源大幅降低，进一步优化了模型的运行效率。此外，特征数量从原始的23个（已删除无意义的ID和目标变量）减少至降维后的18个主成分。这一降维过程不仅简化了模型结构，降低了模型复杂度，还减少了过拟合的风险，同时保留了数据的核心信息，为模型的高效运行和准确预测提供了有力支持。

综上所述，PCA降维在本研究中有效地平衡了模型精度、训练效率和内存资源消耗间的关系，为高维医疗数据的处理提供了一种可行的解决方案。

图3展示了主成分分析（PCA）的解释方差比例图。从图中可知，随主成分数量增加，解释方差累积值逐步增长。当主成分数量达到17.5时，累积方差接近96%。这表明前17个主成分能够有效捕捉数据中大部分的变异性，为降维后的模型提供了足够信息量，同时减少了数据冗余。

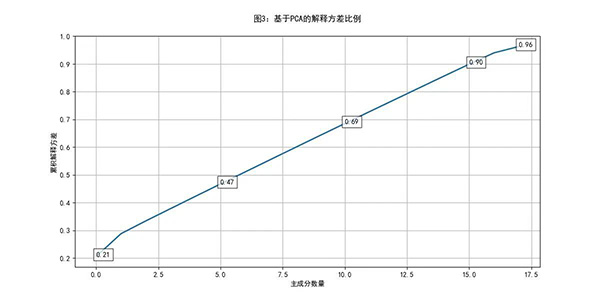
图4则呈现了前两个主成分的特征贡献情况。从图中可以清晰地看到，这两个主成分之间相互独立，不存在线性相关性。这种独立性是PCA降维的关键优势之一，它确保了降维后的数据特征能够更有效地反映原始数据的内在结构，同时避免了信息的重复表达。在高维数据处理中，这种独立性尤为重要，因为它能够确保每个主成分都能为模型提供独特的价值。

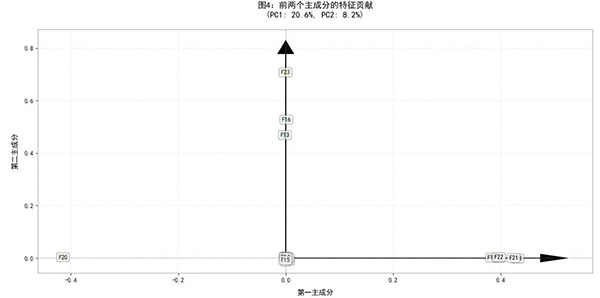
通过图3和图4，可以直观地评估PCA降维效果。累积方差的快速增长和主成分的独立性表明PCA在本研究中是一种有效的降维方法，能够在保留关键信息的同时显著降低数据维度，提高模型的运行效率和可解释性。

图5展示了前10个主成分的特征权重热力图。图中清晰地呈现了各原始特征在不同主成分中的特征权重值。这些权重值反映了每个特征在各个主成分中的贡献程度，揭示了不同特征与主成分之间的线性关系。权重值的大小和分布表明了哪些特征对特定主成分的形成更为关键，同时也揭示了特征之间在主成分空间中的相对重要性。

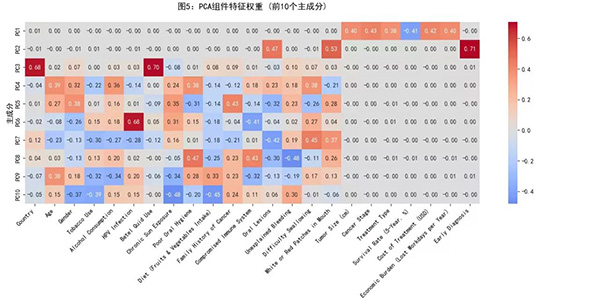
热力图通过颜色的深浅直观地显示了特征权重的大小。颜色越深（通常为红色或蓝色），表示权重值越大或越小，反映了特征在主成分中的显著性。通过分析特征权重热力图，可以更好地理解模型的决策依据。例如，在医疗数据中，某些特征可能在特定主成分中权重较高，这可能提示这些特征与某种疾病特征或病理过程密切相关，从而为临床诊断和研究提供有价值的线索。

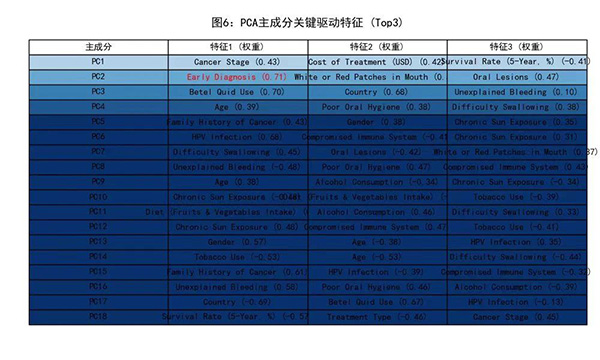
图6则展示了每个主成分中的前3个关键驱动特征值，设定大于0.7的特征值以红色显示。

ROC曲线下面积（AUC）是评估模型预测效能的重要指标。如图7所示，本研究比较了基于原始数据和PCA降维数据构建的口腔癌诊断预测模型的ROC曲线及其AUC值。结果显示，两种模型的ROC曲线完全重合，且AUC值均达到1.0的理想值。这一结果表明：（1）两种模型在口腔癌诊断中均表现出优异的判别能力；（2）PCA降维处理并未影响模型的分类性能；（3）无论是否经过特征降维，模型均能准确区分口腔癌患者与非口腔癌患者对照。这种优异的预测性能可能归因于特征变量的强判别力以及模型架构的优化设计，为临床口腔癌的早期诊断提供了有效的决策支持工具。

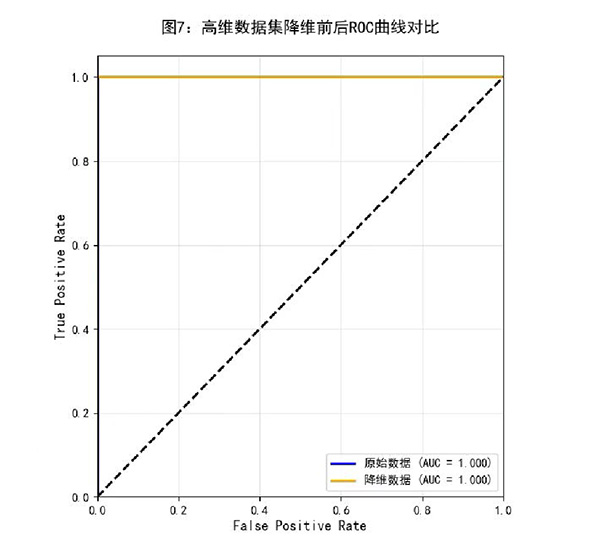
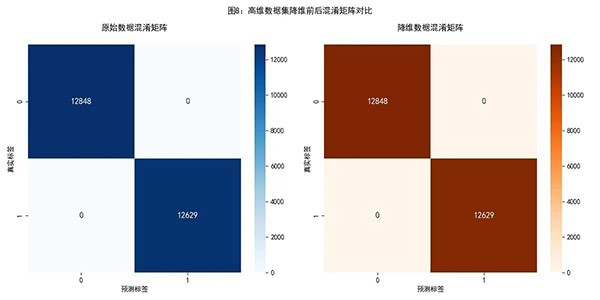
图8展示了基于原始数据和PCA降维数据构建的预测模型的分类混淆矩阵。其中，0代表非口腔癌患者，1代表口腔癌患者，横轴为预测结果，纵轴为真实标签。从图中可知，降维前后的模型分类表现完全一致：所有真实标签为0的样本均被准确预测为0，真实标签为1的样本均被准确预测为1。两个模型既未出现误诊（假阳性）也未发生漏诊（假阴性）。这一结果进一步证实，PCA降维处理在保持模型预测性能方面具有可靠性，即使在降维后，模型的分类精度也未受到任何影响。

四 研究结果与展望

本研究通过具体实例深入探讨了PCA降维技术在高维医疗数据中的应用。当前研究的核心在于如何从复杂的高维数据中高效提取有价值的信息，降低数据维度，同时确保数据的完整性和准确性。然而，PCA在处理高维医疗数据时仍存在一些局限性。例如，PCA可能会丢失部分重要信息，导致降维后的数据信息量有所减少；此外，其计算复杂度较高，可能限制其在大规模数据集中的应用。

因此，未来的研究可以从以下几方面展开：首先，引入新的数学方法或优化技术，以提升PCA算法的性能，使其在处理复杂数据时更加高效；其次，可结合其他降维方法，如t-SNE等，以进一步优化降维效果，充分发挥不同方法的优势；最后，深入研究降维对诊断精准度的影响，探索如何在降维过程中更好地平衡信息保留与计算效率之间的关系。这些研究方向将有助于我们更精准地处理高维医疗数据，从而进一步提升医疗服务的质量和效率，推动医疗诊断技术的持续进步。

作者简介

安志萍，高级工程师，在职博士学历，专业技术上校退役。CHIMA委员，中国研究型医院学会医疗信息化分会理事，中国医疗保健国际交流促进会医学工程与信息学分会委员，中国医学装备协会医院物联网分会常务委员。长期从事医院信息化建设工作。作者观点纯属与同行做技术交流，欢迎批评指正。